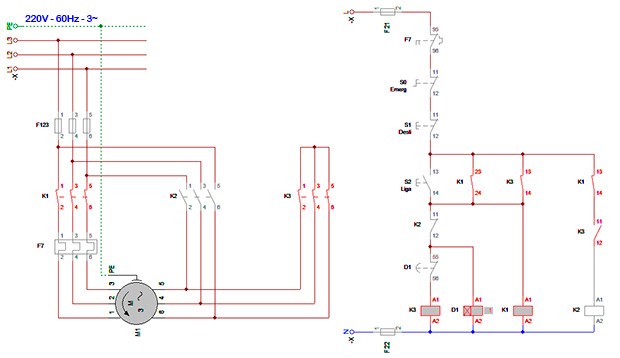
Neste artigo trataremos sobre a mais usual das partidas indiretas de motor elétrico trifásico a partida estrela triângulo.
Ligação Estrela-Triângulo.
Vantagens:
1. Redução da corrente de partida para 1/3 da corrente nominal;
2. Baixo custo;
3. Componentes da chave ocupam pouco espaço (quadro elétrico pequeno);
4. Sem limitação no número de partidas.
Desvantagens:
1. Exige um motor de dupla tensão nominal com 6 terminais;
2. A tensão da rede deve coincidir com a tensão em triângulo do motor;
3. Aplicações com partida em vazio ou com carga leve (torque de partida reduzido a 1/3 do nominal);
4. Deve atingir pelo menos 90% da velocidade nominal antes de comutar para triângulo (pico de corrente no momento da comutação);
5. Para partida em triângulo só deve ser comutada após o motor for ligado no mínimo 90%.
Esses motores quando do modelo trifásico utilizam diversos tipos de partida, tendo sido popularizada a estrela-triângulo que tem sido uma das mais utilizadas por sua praticidade e baixos custos (FRANCHI, 2008).
Atualmente existem quatro tipos de diagramas elétricos, sendo eles, o funcional, multifilar, unifilar e trifilar. Podem ser caracterizados como:
O diagrama funcional aborda a parte da instalação elétrica, possibilita uma fácil e rápida representação do que se trata o funcionamento do equipamento, também dispõe todos os componentes e os condutores do circuito elétrico.
Figura 1: Diagrama Funcional.
 |
| Fonte: Mundo da Elétrica, 2018. |
Figura 2: Diagrama Multifilar.
 |
| Fonte: Telcurso, 2017. |
O diagrama unifilar é o mais utilizado em obras, ele é esboçado encima da planta arquitetônica, exibindo os dispositivos e trajeto dos condutores severamente colocado em seus respectivos lugares, em 2D.
Figura 3: Diagrama Unifilar.
 |
| Fonte: Sala de Elétrica, 2017. |
O diagrama trifilar é bastante usado em equipamentos trifásicos e sistemas de comandos elétricos. Cada uma das três fases de sistema elétrico pode ser representado pelo diagrama trifilar, que tem seus detalhes na posição vertical.
Figura 4: Diagrama Trifilar.
 |
| Fonte: SlidePlayer, 2015. |
Foi feita uma simulação em estrela triangulo que está disponível pelo link : Ligação Estrela-Triângulo
Podemos representar os números complexos de duas formas, na forma polar e retangular.
Na forma retangular, temos que a e b são representantes do eixo real e o imaginário.
P = a + jb
E na forma polar, há o módulo e o ângulo, respectivamente, P e ?.
P = P ? ?
Definição de Potência Ativa, Reativa e Aparente.
A potência ativa, que é dada em watts (W) ou kilowatts (KW), pode ser medida pelo aparelho que realiza essas medições, normalmente chamado de kilowattimetro, será a energia que de fato, será utilizada.
A potência reativa trabalha no meio do gerador de energia e a carga entre eles, pois tem a função de conservar o campo eletromagnético operante do motor, lâmpadas fluorescentes, transformadores, etc. Sua unidade de medida é feita em kvar, que quer dizer kilovolts-Amperes-Reativos.
A potência aparente, aponta se a quantidade de energia utilizada é o bastante para um determinado fornecimento elétrico, assim pode indicar onde há carência de fornecimento, que tem sua medida em kilovolts-amperes, o VA é o que chamamos de potência aparente, ela é resultado da soma fasorial (vetorial) da potência ativa em watts (W) e da potência reativa (var).
? Tensão de Fase (Vf) = Segundo Diogo Souza (2018, p. 43) a "tensão presente em apenas uma das impedâncias (no caso de cargas), ou a apenas uma das três fontes geradoras (no caso de geradores)."
? Corrente de Fase (If) = Segundo Diogo Souza (2018, p. 43) a "corrente que percorre as impedâncias (no caso de cargas), ou que percorre as três fontes geradoras (no caso de geradores)."
? Tensão de Linha (Vl) = Segundo Diogo Souza (2018, p. 44) se refere a "diferença de potencial entre as fases."
? Corrente de Linha (Il) = Segundo Diogo Souza (2018, p. 44) é a "corrente que percorre as linhas de transporte de energia."
O que é PU (Sistema por Unidade)?
Algumas vezes os valores de tensão, corrente, impedâncias e potencias de um circuito são escritas em valores de pu associado em valores de referência, ou também em percentagem.
Existem dois tipos, sendo eles em pu ou em percentagem.
Pu = Quantidade dada / quantidade base
% = (Quantidade dada / quantidade base) * 100
Triângulo
Podemos representar os números complexos de duas formas, na forma polar e retangular.
Na forma retangular, temos que a e b são representantes do eixo real e o imaginário.
P = a + jb
E na forma polar, há o módulo e o ângulo, respectivamente, P e ?.
P = P ? ?
Figura 5: Número complexo na forma retangular (a) e polar (b).
 |
| Fonte: Ufrgs, 2018. |
Definição de Potência Ativa, Reativa e Aparente.
A potência ativa, que é dada em watts (W) ou kilowatts (KW), pode ser medida pelo aparelho que realiza essas medições, normalmente chamado de kilowattimetro, será a energia que de fato, será utilizada.
A potência reativa trabalha no meio do gerador de energia e a carga entre eles, pois tem a função de conservar o campo eletromagnético operante do motor, lâmpadas fluorescentes, transformadores, etc. Sua unidade de medida é feita em kvar, que quer dizer kilovolts-Amperes-Reativos.
A potência aparente, aponta se a quantidade de energia utilizada é o bastante para um determinado fornecimento elétrico, assim pode indicar onde há carência de fornecimento, que tem sua medida em kilovolts-amperes, o VA é o que chamamos de potência aparente, ela é resultado da soma fasorial (vetorial) da potência ativa em watts (W) e da potência reativa (var).
Figura 6: Relação entre kW, kvar e kVA.
 |
| Fonte: Engelétrica, 2011. |
? Tensão de Fase (Vf) = Segundo Diogo Souza (2018, p. 43) a "tensão presente em apenas uma das impedâncias (no caso de cargas), ou a apenas uma das três fontes geradoras (no caso de geradores)."
? Corrente de Fase (If) = Segundo Diogo Souza (2018, p. 43) a "corrente que percorre as impedâncias (no caso de cargas), ou que percorre as três fontes geradoras (no caso de geradores)."
? Tensão de Linha (Vl) = Segundo Diogo Souza (2018, p. 44) se refere a "diferença de potencial entre as fases."
? Corrente de Linha (Il) = Segundo Diogo Souza (2018, p. 44) é a "corrente que percorre as linhas de transporte de energia."
O que é PU (Sistema por Unidade)?
Algumas vezes os valores de tensão, corrente, impedâncias e potencias de um circuito são escritas em valores de pu associado em valores de referência, ou também em percentagem.
Existem dois tipos, sendo eles em pu ou em percentagem.
Pu = Quantidade dada / quantidade base
% = (Quantidade dada / quantidade base) * 100
PU (Sistema por Unidade)
VBase = 127 v
Vl = 220 v
Vl = 220 / 127 = 1,73 PU ou 173 %
Vf = 127 v
Vf = 127 / 127 = 1 PU ou 100 %
Estrela
Impedância Retangular
ZBase = 6,35 + j 11
ZBase = 6,35 + j 11 / 6,35 + j 11 = 1 PU ou 100 %
Impedância Polar
ZbasePolar = 12,7 ? 60°
ZbasePolar = 12,7 ? 60° / 12,7 ? 60° = 1 PU ou 100 %
If = 127 ? 0° / 12,7 ? 60°
If = 10 ? -60°
IfBase = 10 ? -60° / 10 ? -60° = 1 PU ou 100 %
If = 10 ? -60°
Il = If = 1.73 x 10 ? -60° = 17,32 ? -60°
Il = 17,32 ? -60° / 10 ? -60° = 1,73 PU ou 173 %
Vl = Vf
Potência Aparente (3 * Vf * Vl)
3 * 220 * 17,32 = 11.430 VA
Potência Base = 11.430 VA
Potência Ativa (3 * Vf * If * Cos f -60)
3 * 220 * 17,32 * Cos f -60° = 5710 W
